[Paper Review] Densely Connected Convolutional Networks

1. Abstract

• 최근 ConvNet 관련된 연구를 보니 그 깊이가 깊을수록 정확도가 좋아지지만, 입력-출력 사이의 connection이 적으면 학습에 효율적이었다고 합니다.
• 그래서 DenseNet에서는 그 깊이를 줄이고, 모든 layer를 feed-forward하게 연결해주었다고 합니다.
• L 개의 layer에 대해 ConvNet에서 L 개의 connection이 있다고 하면, DenseNet에서는 $ \frac{L(L + 1)}{2} $ 개의 connection이 생깁니다.
• 이를 통해
  1. gradient-vanishing을 해결하고
  2. feature propagation을 강화했으며
  3. feature의 재사용을 encourage(?)하고
  4. parameter의 수를 감소 시켰다고 합니다.
• CIFAR 10, CIFAR 100, SVHN, ImageNet 등에서 SOTA 를 기록했다고 합니다.

2. Introduction

• 현재 연구는 앞의 layer에서 뒤의 layer로 가는 짧은 경로를 만들어내는 쪽에 초점을 맞추고 있다고 합니다. DenseNet에서는 이를 녹여내어 모든 Layer를 연결해보았다고 합니다. 기존의 ResNet은 x와 H(x)를 더해주었다면, DensNet에서는 concat해줌으로서 depth를 늘려갑니다.
• abstract에서 언급된 DenseNet의 효과 중 4번에 의문을 가진 분들이 좀 있으실 겁니다. "아니, layer를 전부 이어줬는데 그게 어떻게 parameter 감소로 이어지지?" 하고요. 이는 DensNet이 불필요한 feature를 다시 학습할 필요가 없기 때문이라고 합니다.
• 최근 연구에 따르면 ResNet에서 상당히 일부 레이어만 학습에 관여한다고 하고, 심지어 몇 레이어를 제외하고 학습시켜도 비슷한 성능을 냈다고 합니다.
• DenseNet은 매우 좁은 feature map을 가지는데, 이는 feature map들을 바꾸지 않고 보존하는 "collective knowledge" 를 도입하고, 마지막 분류기에서 feature map들로부터 결정을 내림으로서 가능했습니다.
• 가장 큰 장점은 gradient의 흐름을 개선했고, 모든 레이어가 loss function 과 입력에 직접 맞닿아 있어 학습 시키기에 매우 용이했단 점이라고 합니다.

3. DenseNets

architecture of DenseNet

notation

• $x_{0}$ 는 convNet에 처음 들어가는 한 개의 image 입니다.
• 네트워크는 L 개의 layer로 구성되어 있고, 각 l 번째 layer는 비선형 변환 $H_{l}(\cdot)$ 과 BN, activation function 등으로 이루어져 있습니다.
• $l^{th}$ layer의 출력 feature map 을 $x_{l}$이라고 하겠습니다.

ResNets

• residual : $x_{l} = H_{l}(x_{l-1}) +x_{l-1}$
• residual block을 통해 전 layer의 출력을 다음 layer의 입력으로 넣어주어 gradient가 직접 전해질 수 있게 하는 것이 ResNet의 장점입니다.
• 하지만 identity function과 $H_{l}$이 합쳐짐으로서 정보의 흐름을 막을 수 있다고 합니다.

Dense connectivity

• $l^{th}$ layer가 $x_{0}, x_{1}, ..., x_{l-1}$을 입력으로 받고 이는 $x_{l} = H_{l}([x_{0}, x_{1}, ..., x_{l - 1}])$ 와 같이 표현될 수 있습니다.
• 이러한 Dense connectivity로 인해 본 논문에서 제안하는 모델의 이름이 DenseNet이라고 합니다.

Composite function

• $H_{l}$을 BN - ReLU - 3x3 convolution의 순서로 정의했습니다.

Pooling Layers

• 만약 $x_{l} = H_{l}([x_{0}, x_{1}, ..., x_{l - 1}])$ 에서 각 feature map 간의 크기가 다르다면 하나의 커널로 계산할 수 없을 것입니다.
• 그렇지만, CNN의 가장 큰 부분은 바로 featuremap의 크기를 변화시키는 down sampling 입니다.
• 하나의 커널로 연산하기 위해, 또 CNN의 성질을 잃게 하지 않기 위해 dense block이라는 것을 정의했다고 합니다.
• 하나의 dense block에서 나온 출력을 1x1 kernel로 conv해주고, (2, 2) kernel로 avg pooling을 해 다음 block에 넘겨줬다고 합니다.
• 이러면 각 dense block에서 feature의 크기도 유지하고 convnet의 성질도 보존할 수 있습니다.

Growth rate

• 각 비선형 변환 $H_{l}$에서는 k 개의 feature map을 형성하는데, 따라서 $l^{th}$ layer에서 $k_{0} + k(l-1)$ 개의 feature map을 입력으로 받게 됩니다.
• 기존 ConvNet과 DenseNet의 가장 큰 차이점은 굉장히 적은 feature map(k = 12)를 만든다는 것입니다.
• k를 groth rate 라는 hyperparameter로 정의하였습니다.
• 각 layer에서 출력으로 나온 feature map을 collective knowledge에 저장하고, 이는 네트워크의 전역 상태로도 볼 수 있게 됩니다. 이는 정말로 "전역적"이어서 모델에서 모델로 넘겨줄 과정이 필요 없이 어디서든 접근할 수 있다고 합니다.

Bottleneck Layers

• 1x1 conv

Compression

• .

Implementation Details

Implementation Details

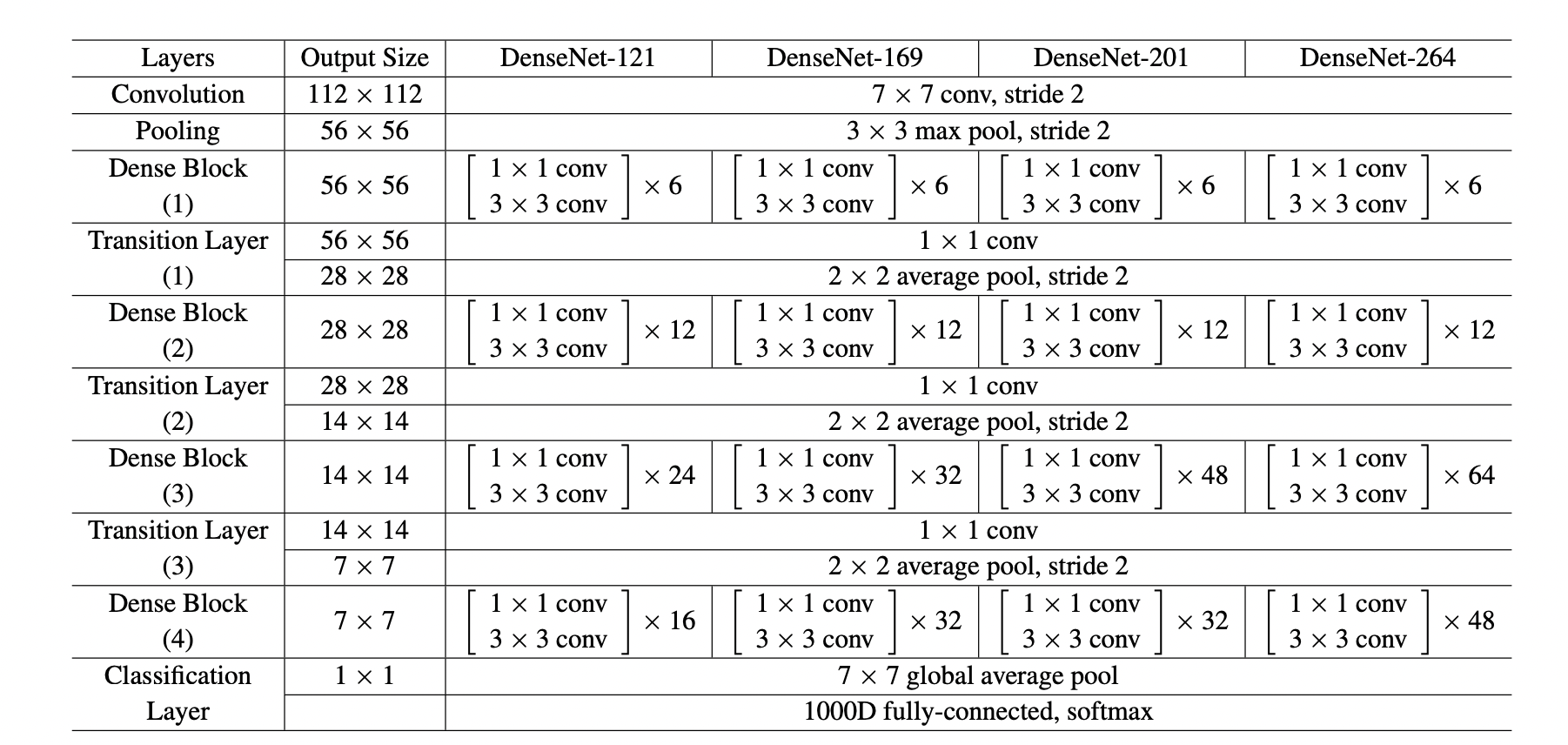
4. Results

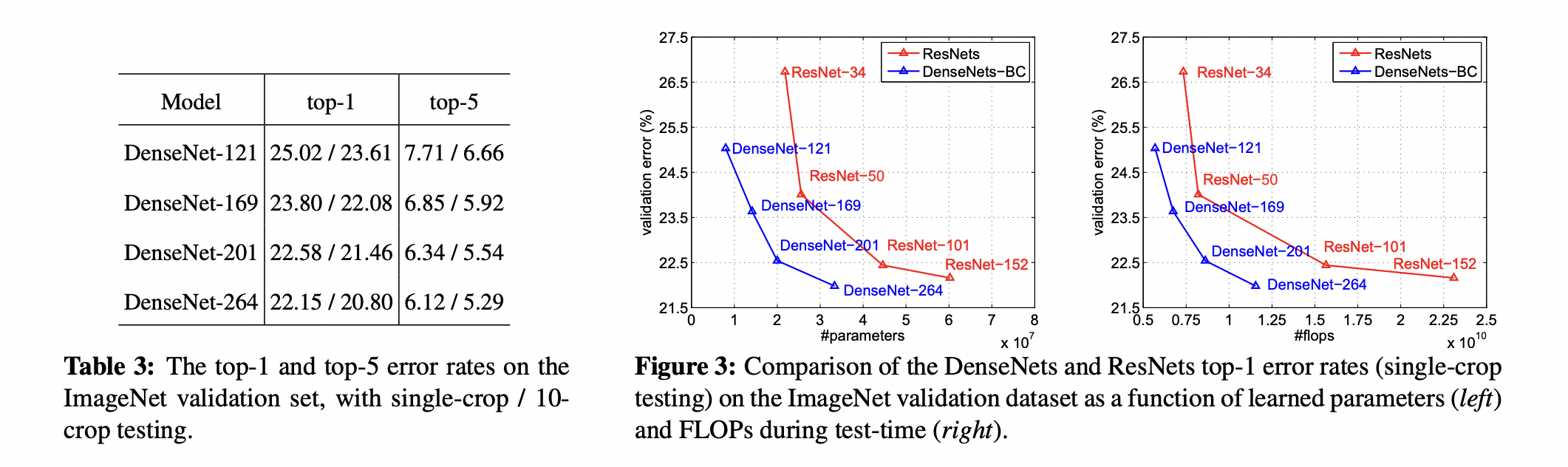
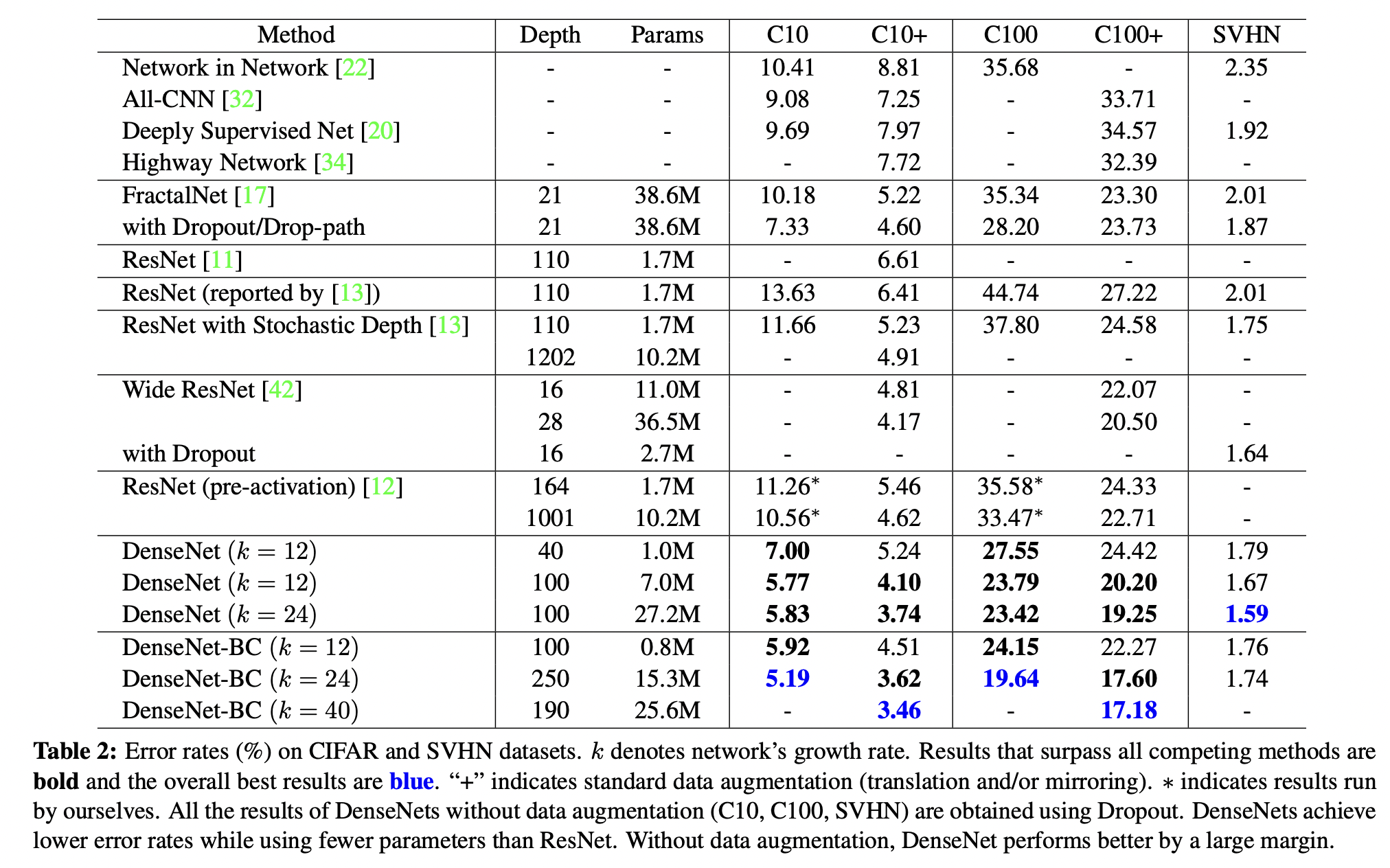
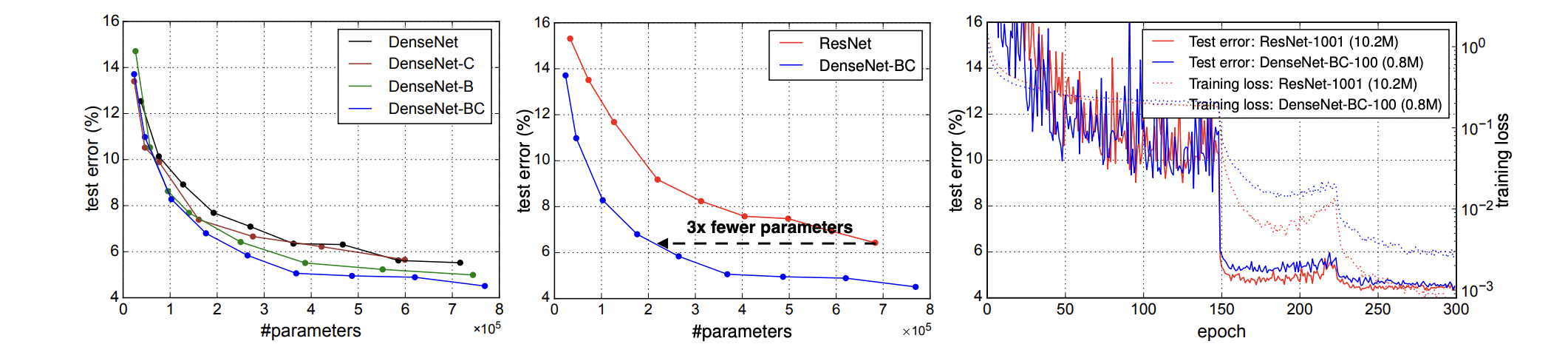
5. Discussion

Model compactness

• 앞선 layer들에서 추출된 모든 feature map에 접근할 수 있어서 이들을 모두 재사용할 수 있고, 이는 model의 compactness를 향상시켰다고 합니다.

Implicit Deep Supervision

• 기존 ConvNet에 비해 loss function과의 짧은 connection으로부터 supervision을 받음으로서 성능이 향상되었다고 생각한다 합니다.
• 2~3 단계만 거치면 모든 layer가 loss function과 직접적으로 맞닿아 있기에 loss function과 gradient가 다소 덜 복잡한 구조를 지닌다고 합니다.

Stochastic vs Deterministic Connection

• stochastic depth regularization와 dense convolutional network 사이에 연관성이 있다고 합니다.
• 전자에서 residual network의 layer가 임의로 무시되고 이는 근처의 layer간의 직접적인 connection을 만들었습니다. pooling layer는 무시되지 않았기에(구조를 깰 수 있으므로?) 이는 DenseNet과 유사한 구조를 만들었다고 합니다.

Feature Reuse

1.모든 layer의 weight는 같은 블럭 내에서 많은 입력에 퍼지게 됩니다.

• 이는 매우 초기에 뽑힌 feature도 아주 깊이 있는 layer에서도 사용된다는 것을 알려줍니다.

2.Transition Layer의 weight도 여러 layer에 퍼지면서 첫 denseNet의 첫 레이어부터 마지막 레이어까지 정보를 전달하게 합니다.

3.2~3 block의 layer들은 transition layer의 output에 적은 weight을 할당합니다.

• 이는 transition layer가 많은 중복된 feature를 뽑아낸다는 것을 의미합니다.

4. classification layer에서도 전체 dense block의 가중치를 사용하지만 마지막 feature map에 상당히 집중된 것을 확인할 수 있습니다.

• 이는 network의 후반부에서 high-level feature를 생성하는 것이라고 생각된다고 합니다.

요약

1. 하나의 dense block에서 모든 layer를 연결하는 구조를 가진 DenseNet을 제안하였습니다.
2. 이는 불필요한 feature의 학습을 줄여 compactness를 향상시켰습니다.
3. 기존의 convNet은 feature를 더해 그 의미를 희석시켰다면, 여기선 concat하여 의미를 보존하면서 pooling layer를 block사이에 두오 depth를 늘려가며 down sampling하는 기존 convNet의 구조를 유지하였습니다.

출처 : https://arxiv.org/pdf/1608.06993.pdf